前面提到，对于第三章引入的 untyped lambda calculus，对一个 term 进行求值可能会有两种结果。第一种结果是我们可以一路将这个 term 求值为一个 value，例如对 iszero 0 求值即可得到 value true；另一种结果是我们会在求值到一半时”卡住“（stuck），这时我们手中的 term 并不是一个 value、但已经没有求值规则可供我们使用了。例如，我们无法进一步对 iszero false 这个 term 进行求值，它既不是一个 value、也没有针对 iszero false 的求值规则。

我们通常并不希望一个程序包含任何无法被求值为 value 的 term，因为这样的程序通常情况下都是错误的程序，运行这些程序得不到任何结果值，是无意义的。有没有什么办法能够让我们识别出这些程序呢？最简单的办法是直接运行这些程序，如果它们在求值的某一步”卡住“了，那么说明其中包含错误。这种方法的缺点非常明显，它需要程序实际运行起来才能得知程序是否包含错误，如果不具备程序运行的条件，则无法判定；另外，对于那些存在外部输入的程序，这种方法只能验证程序运行过的部分是正确的，并不能验证程序的其余部分也是正确的。

我们希望能够在不运行程序的前提下，就知晓这个程序是否正确（即是否不会在运行时”卡住“）。我们可以引入类型（Type）来解决这个问题。我们把程序中的所有 term 归为三类，一类是那些会最终求值为一个整数值的 term，我们称这些 term 具有类型 \mathbf{Nat}；另一类是那些最终会求值为一个 bool 值，我们称这些 term 具有类型 \mathbf{Bool}；最后一类是那些既不具有类型 \mathbf{Nat} 、也不具有类型 \mathbf{Bool} 的 term，我们称这样的 term 为没有类型的 term。如果一个 term t 具有类型 \mathbf{T} ，我们将其写作 t: \mathbf{T} 。

Typing Relation

引入类型来判断一个程序是否正确的最核心的想法是尝试判断表示整个程序的 term 是否具有某一个类型。如果一个 term 具有某一个类型，就说明这个 term 在运行时一定会最终被求值为一个值。如果整个程序的 term 具有某一个类型，就说明这个程序是正确的。因此，我们需要建立一套逻辑系统，为每一个可能的 term 确定判定它具有的类型的方法。我们仍然可以使用熟悉的在 term 上归纳的方法，即基于所有可能的 term 的形式，对每一种形式的 term 所具有的类型进行归纳。

第三章的 untyped lambda calculus 中定义 term 的形式可能如下：

t ::=
	true
	false
	if t then t else t
	0
	succ t
	pred t
	iszero t

对于 true 、false 和 0 这三个最基本的 term 我们可以立即得出它们所具有的类型：

true : Bool
false : Bool
0 : Nat

接下来我们考虑如何为一个 if term 确定它所具有的类型。假定 term 的形式为 \text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3 。回顾 if term 的求值规则，我们需要首先将 t_1 求值为一个 bool 值，然后再根据 bool 值将 if term 分别求值为 t_2 或 t_3 。由于 [/katex]t_1[/katex] 需要能够被求值为一个 bool 值，因此要想 if term 具有某一个类型，必须有 t_1 : \mathbf{Bool} 。当 t_1 被求值为一个 bool 值后，if term 将被求值为 t_1 或 t_2 。那么 if term 的类型是什么呢？如果 t_1 与 t_2 的类型一致，那么显然 if term 的类型就是 t_1 和 t_2 的类型；如果它们的类型不一致，我们则规定这种情况下 if term 没有类型。由于我们无法运行程序得到 t_1 真实的求值结果，因此我们无法提前假定 if term 最终会被求值为哪个 term。

需要注意到的是，判断一个程序是否正确可以等价为判断一个程序是否停机，是非常典型的不可判定问题。因此，无论是以什么方法进行判断，都不能做到在有限的时间内给出完全准确的结果。要想在有限的时间内给出一个结果，必须牺牲准确性。上述的 if term 的类型判定就是一个很典型的例子。在这里，我们会错误地将原本正确的程序判定为错误。

综上，我们可以仿照 evaluation relation，写出 if term 的 typing relation：

\frac{ t_1 : \mathbf{Bool} \;\;\; t_2 : \mathbf{T} \;\;\; t_3 : \mathbf{T} }{ \text{if}\;t_1\text{then}\;t_2\;\text{else}\;t_3 : \mathbf{T} }

上面的表示方法的含义即，如果 t_1 具有类型 \mathbf{Bool} 、t_2 和 t_3 都具有相同的类型类型 \mathbf{T} ，那么 term \text{if}\;t_1\text{then}\;t_2\;\text{else}\;t_3 具有类型 \mathbf{T} 。

类似地，我们也可以得到其他所有 term 的 typing relation，总结为：

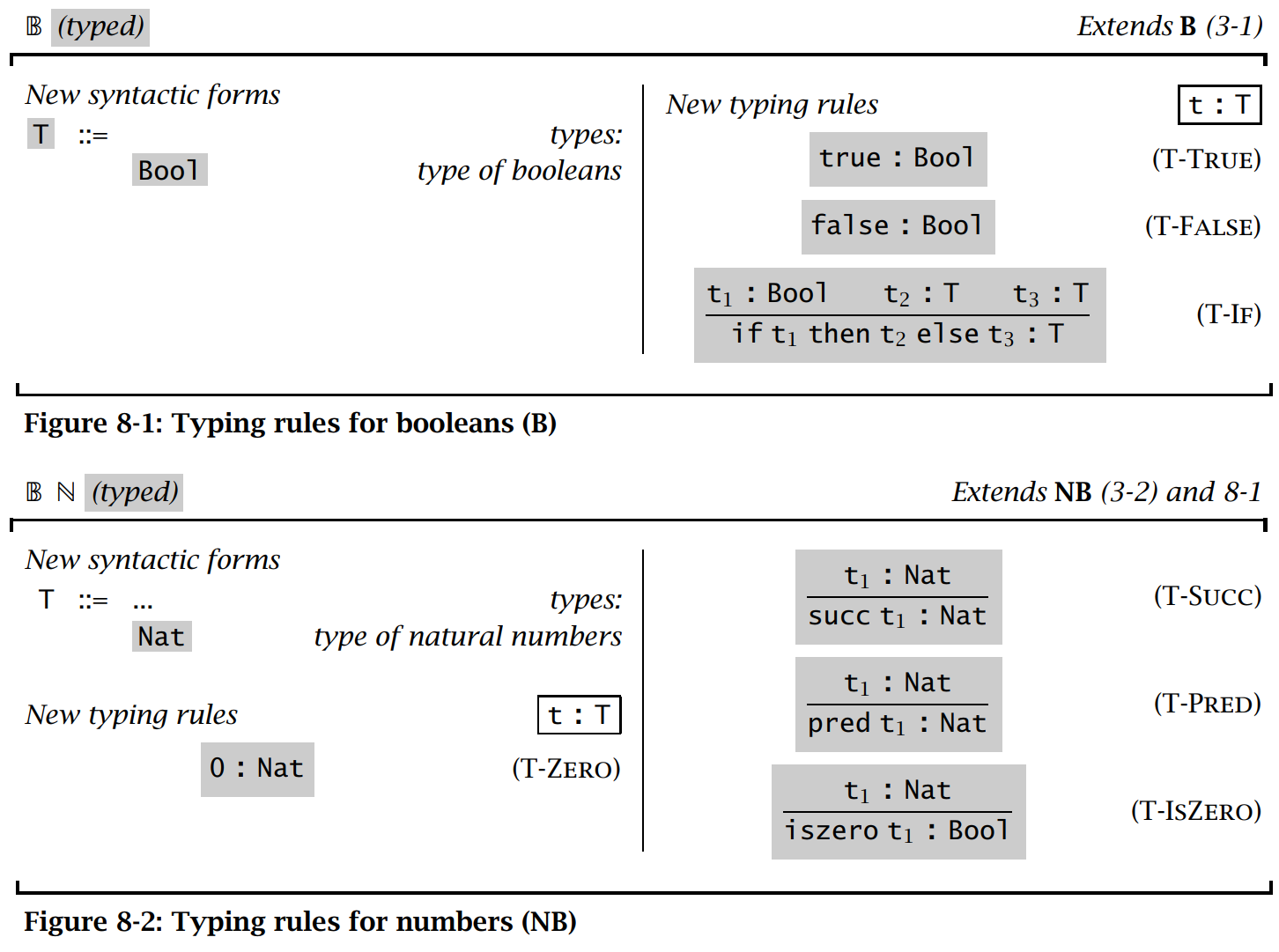
Typing relation 给出了一个从更小的 term 的类型推导更大的 term 的类型的方法。实际上，将 typing relation 中的 premises 和 conclusion 进行交换后得到的推导式仍然成立。例如，我们有：

\frac{ \text{succ}\;t_1 : \mathbf{Nat} }{ t_1 : \mathbf{Nat} }

\frac{ \text{pred}\;t_1 : \mathbf{Nat} }{ t_1 : \mathbf{Nat} }

\frac{ \text{iszero}\;t_1 : \mathbf{Bool} }{ t_1 : \mathbf{Nat} }

\frac{ \text{if}\;t_1\text{then}\;t_2\;\text{else}\;t_3 : \mathbf{T} }{ t_1 : \mathbf{Bool} \;\;\; t_2 : \mathbf{T} \;\;\; t_3 : \mathbf{T} }

与 derivation tree 类似，为判定一个 term 的类型，也可以画出一棵 typing derivation tree，如下图所示。

很容易证明，如果一个 term 有类型，那么它的类型是唯一的，且它的 typing derivation tree 也是唯一的。需要注意到的是，这一条性质仅在本章提出的简单类型系统中有效；在后续章节的类型系统中，一个 term 将有可能有多个类型，且推导一个 term 所产生的 typing derivation tree 也可能不唯一。

Safety = Progress + Preservation

前面我们提到，引入类型系统的目的是为了帮助我们判断一个程序是否正确。在这里，我们评判一个程序是否正确的标准并非它完成了我们希望它执行的任务，而是它在执行过程中不会”卡住“，不会产生没有对应求值规则的 term 。我们希望，如果一个 term 具有某个类型，那么它一定能最终被求值为一个值。如果表示整个程序的 term 具有某个类型，那么这个程序则是正确的。也就是说，类型系统最重要的属性是 safety：一个 term 如果被类型系统判定具有某个类型，那么它一定是正确的。也有许多人把这个属性称为 soundness。但反之，如果一个 term 被类型系统判定不具有类型，那么它不一定是错误的。例如，当 t_2 和 t_3 的类型不一致时，虽然 \text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3 没有类型，但它仍然可能是正确的。

我们可以通过证明两个定理来证明我们的类型系统确实是 safe 或 sound 的。第一个定理称作 progress 定理：

【Progress 定理】一个具有类型的 term 一定不会”卡住“。这个 term 要么是一个值、要么存在一个求值规则能对其进行求值。

第二个定理称作 preservation 定理：

【Preservation 定理】一个具有类型的 term 在单步求值后得到的 term 一定也具有类型。

显然，progress 定理保证了任何一个有类型的 term 都要么是值、要么能被至少求值一步；preservation 定理保证了有类型的 term 经过一步求值后得到的 term 要么是值、要么仍然能够继续被求值。因此，这两个定理保证任何一个有类型的 term 都一定能被求值为一个值。

原书花费了大量篇幅对这两个定理进行证明。证明的思路非常简单，核心思想仍然是 induction on terms 。在此不做进一步介绍，如果您感兴趣可以参考原书进行学习。