在第五章中引入的 untyped pure lambda-calculus 中，所有的变量都有一个符号名称，例如 x、y、s 和 t 等。然而，在执行 substitution 时，这些为变量指派的符号名称有可能发生冲突，导致原本的约束变量被更改为自由变量或原本的自由变量被更改为自由变量，这一点我们已经在第五章中进行了介绍和讨论。我们当时提出的解决方案是在执行 substitution 前，对会产生冲突的约束变量进行重命名，使得重命名后的符号名称不会发生冲突。这种执行 substitution 的方法称为 substitution up to renaming of bound variables。

当我们需要使用真实的程序设计语言实现 pure lambda-calculus 的求值时，我们必须将上述的在 substitution 过程中防止符号名称冲突的过程考虑在内。具体而言，我们必须考虑如何在宿主语言中表示出一个变量。可以有以下几种表示方式：

• 仍然使用一个符号名称表示一个变量，但是在执行 substitution 时，必须显式地执行一步操作，这步操作将语句中的约束变量的符号名称重命名为一个没有用到过的名称以防止名称冲突；
• 仍然使用一个符号名称表示一个变量，但是同时要求所有的约束变量的符号名称必须与其他约束变量的符号名称以及所有可能会用到的自由变量的符号名称不同。这个要求被称为 Barendregt convention。在这种情况下，执行 substitution 时不需要对约束变量进行重命名，因为符号名称冲突一定不会发生；但是在每一轮 substitution 后可能需要执行一轮重命名以维持约束条件。例如，对于 substitution \left[x \mapsto \lambda y.\; y\right] x\; \lambda y.\; y，虽然在 substitution 前的语句 x\; \lambda y.\; y 满足 Barendregt convention，但是在 substitution 后的结果语句 \left(\lambda y.\; y\right) \lambda y.\; y 不满足 Barendregt convention，需要执行一轮重命名以维持约束条件；
• 不使用符号名称来表示一个变量，而是使用一种 canonical 的变量表示方式；使用这种方式，在任何情况下都不需要对变量进行重命名；
• 可以使用类似于 explicit substitutions 等机制，完全避免 substitution；
• 如果需要实现的语言完全基于组合逻辑（combinatory logic），那么我们可以完全消除语言中对变量的使用。

本书中采用上述第三种方式。本章会对上述第三种方式中提到的对变量的 canonical 的表示方式进行介绍。

Terms and Contexts

我们不使用符号名称来表示一个变量，而是让变量在其使用的地方直接指向引入该变量的 binder。具体来说，我们使用一个整数来表示一个变量，该整数表示从当前位置开始，变量是从哪一层 abstraction 的 binder 被引入的，0 表示第一层 abstraction。

例如，考虑 identity 组合子 \lambda x.\; x，我们可以按照上述方式将其写作 \lambda .\; 0，注意 \lambda 符号后已经没有表示变量的符号；又例如，考虑组合子 \lambda x.\; \lambda y.\; x\; \left(y\; x\right)，我们可以按照上述方式将其写作 \lambda .\; \lambda .\; 1\; \left(0\; 1\right)。我们将按照传统方式表示的 term，例如 \lambda x.\; x 和 \lambda x.\; \lambda y.\; x\; \left(y\; x\right) 等，称作 ordinary term；将按照上述方式表示的 term，例如 \lambda .\; 0 和 \lambda .\; \lambda .\; 1\; \left(0\; 1\right) 等，称作 nameless term，也可称作 de Bruijn term。Nameless term 中用于表示各个变量的整数称为 de Bruijn index，在编译器的实现中也被称为 static distance。

Syntax

以下三组规则递归地定义出了 nameless term 的完整 syntax：

1. k \in T_n \; \left(0 \le k < n \right);
2. 如果 t_1 \in T_n 且 n>0，那么有 \lambda .\; t_1 \in T_{n-1}；
3. 如果 t_1 \in T_n 且 t_2 \in T_n，那么有 \left(t_1\; t_2\right) \in T_n。

需要注意，nameless term 的完整 syntax 被定义为一族集合 \left\{T_0, T_1, T_2, \cdots\right\} 的并集。T_i 中的 term 符合下列性质：在这些 term 最外层包裹上至多 i 层 abstraction 后，这些 term 将均为组合子。这个性质可以很容易地从上述三组规则中得到验证。另外，我们还可以立即得出推论，即 T_0 中的 term 均为组合子。

Naming Context

前面我们只讨论了 term 中没有自由变量的情况。如果 term 中存在自由变量，那么我们需要借助 naming context 才能够为这些自由变量确定它们的 de Bruijn index。Naming context 是一个从变量的符号名到变量的 de Bruijn index 的映射：

\begin{aligned} \Gamma =\; & x \mapsto 4 \\ & y \mapsto 3 \\ & z \mapsto 2 \\ & a \mapsto 1 \\ & b \mapsto 0 \end{aligned}

对于一个自由变量，我们直接将其 de Bruijn index 确定为 naming context 中对应的值即可。例如，在 \Gamma 下，\lambda x.\; y\; x 的 nameless term 为 \lambda .\; 3\; 0，因为 \Gamma 将自由变量 y 映射为 3。

需要注意，naming context 一定是将 n 个自由变量双射到区间 \left[0, n-1\right] 中的 de Bruijn index 上。因此，我们可以将 naming context 进一步简写为：

\Gamma = x\;y\;z\;a\;b

上述对 \Gamma 的两种写法完全等价。注意在简写的形式中，自由变量从左到右所映射到的 de Bruijn index 是递减的，处于最末尾的自由变量的 de Bruijn index 是 0。在一个 naming context \Gamma 中存在映射的自由变量的集合记做 \text{dom}\left(\Gamma\right)，例如在上述例子中 \text{dom}\left(\Gamma\right) = \left{x,y,z,a,b\right}。

Shifting and Substitution

这一节中将介绍如何在 nameless term 上执行 substitution 操作。

Shifting

回顾在 pure lambda-calculus 中求值一个 application 的过程：

\left(\lambda x.\; t\right)\; s \rightarrow \left[x \mapsto s\right]t

但是，上述过程不能直接用于求值使用 nameless term 表示的 term，即：

\left(\lambda .\; t\right) s\rightarrow \left[0 \mapsto s\right]t

是错误的。原因有两点：

• 将 t 中的 0 替换为 s 是错误的。如果 t 中包含 abstraction，那么这将导致我们将错误的变量进行了替换。此时，t 中的 0 所引用的 binder 是由 t 内部的某个 abstraction 的 binder。例如，在上述的 application 中，对于 t = \lambda .\; 0，执行 \left[0 \mapsto s\right]t 将得到错误的 application 结果 \lambda .\; s，而不是正确的 application 结果 \lambda .\; 0，正确的求值如下：

\begin{aligned} \left(\lambda.\; \underline{t}\right)\; s =\;& \underline{\left(\lambda.\; \lambda.\; 0\right)\; s} \\ \rightarrow\;& \lambda.\; 0 \end{aligned}

• t 中原有的自由变量可能会在 substitution 结束之后引用错误的 binder，因为在 substitution 结束后，我们将 t 从一个 abstraction 中“抽取”了出来，因此我们需要将 t 中的自由变量的 de Bruijn index 递减以保证这些自由变量仍旧引用在若干层外包裹 t 的 abstraction 所引入的 binder。例如，在上述的 application 中，对于 t = 1，执行 \left[0 \mapsto s\right]t 将得到错误的 application 结果 1，而不是正确的 application 结果 0，正确的求值如下：

\begin{aligned} \left(\lambda.\; \underline{t}\right)\; s =\;& \underline{\left(\lambda.\; 1\right)\; s} \\ \rightarrow\;& 0 \end{aligned}

换言之，在 substitution 时，每次跨越一个 abstraction 的边界时，都需要对 term 中的各个 de Bruijn index 进行调整，确保它们一直引用正确的 binder。这个对一个 term 中的 de Bruijn index 进行调整的过程称为 shifting。Shifting 操作用如下的记号表示：

\uparrow_{c}^{d}t

表示将 t 中所有的 de Bruijn index 不小于 c 的变量的 de Bruijn index 加上 d。其操作规则如下：

\begin{aligned} \uparrow_d^c k &= k & \left(k < d\right) \\  \uparrow_d^c k &= k+c & \left(k \ge d\right) \\ \uparrow_d^c \lambda.\; k &= \lambda.\; \uparrow_{d+1}^c k \\ \uparrow_d^c \left(t_1\; t_2\right) &= \left(\uparrow_d^c t_1\; \uparrow_d^c t_2\right) \end{aligned}

同样地，我们需要考虑在跨越 abstraction 边界时对 shifting 的影响。上述规则应该比较容易理解，在此不再赘述。我们进一步将 \uparrow_0^d t 简写为 \uparrow^d t。

Substitution

利用 shifting 操作，可以得到执行 substitution 的方法：

\begin{aligned} \left[j \mapsto s\right]k &= s & \left(k=j\right) \\ \left[j \mapsto s\right]k &= k & \left(k \ne j\right) \\ \left[j \mapsto s\right]\left(\lambda.\; t\right) &= \lambda.\; \left[j+1 \mapsto \uparrow^{1}s\right]t \\ \left[j \mapsto s\right] \left(t_1\; t_2\right) &= \left(\left[j \mapsto s\right]t_1\; \left[j \mapsto s\right]t_2\right) \end{aligned}

Evaluation

第五章介绍了 pure lambda-calculus 的求值规则：

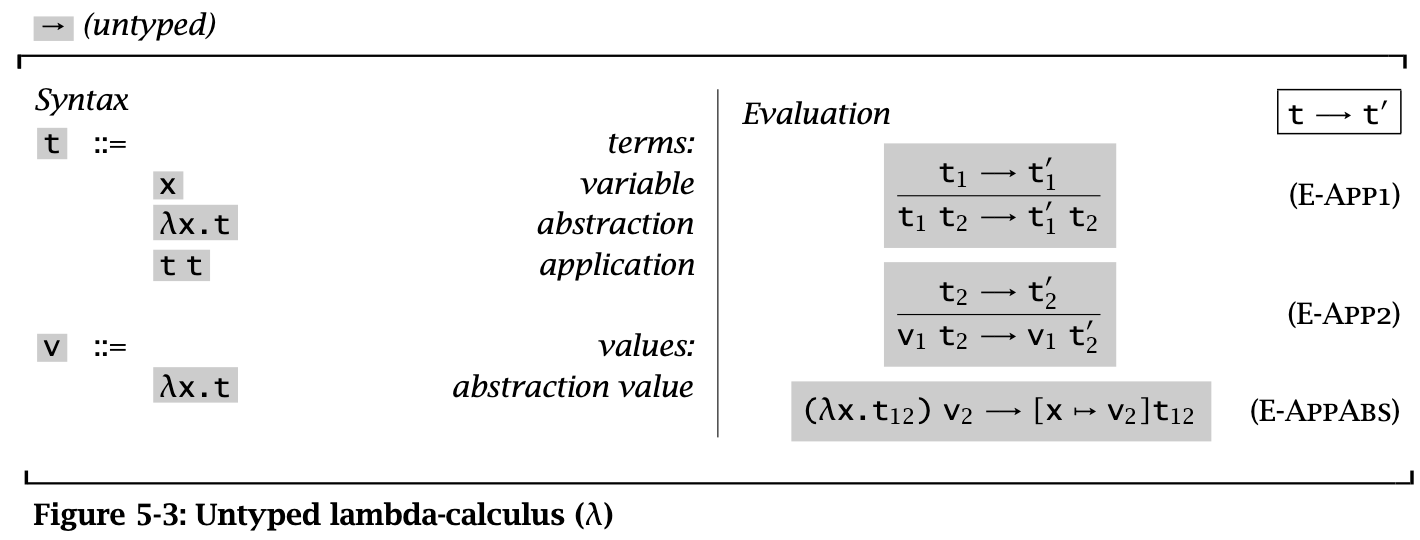
使用 nameless term 表示的 pure lambda-calculus 的求值规则与上面的求值规则大体一致。但是，E-AppAbs 规则需要修改为下列形式：

\begin{aligned} \left(\lambda.\; t_{12}\right)\;v_2 \rightarrow \uparrow^{-1} \left(\left[0 \mapsto \uparrow^1 \left(v_2\right)\right]t_{12}\right) \end{aligned}

这是因为，在应用 E-AppAbs 求值规则后，t_{12} 从一个 abstraction 中被“抽取”了出来，因此需要将结果中的所有 de Bruijn index 递减以保证这些变量仍然引用正确的 binder。