本章给出了一个非常简单的 mini language，其 abstract syntax 如下：

t ::=
	true
	false
	if t then t else t
	0
	succ t
	pred t
	iszero t

围绕这样一个简单的 mini language 进行讨论，本章介绍了如下的重要概念和工具：

• Syntax 的定义，以及如何利用数学归纳法证明 syntax 的某些属性；
• Semantics 的三种分类，即 operational semantics、denotational semantics 以及 axiomatic semantics；
• 如何定义语言的 operational semantics，即如何定义语言的 evaluation rules。

Syntax

定义一个语言的 syntax 即定义这门语言中合法的语句（term）的集合。

我们可以通过 grammar 来定义语言的 syntax。一个语言的 grammar 定义如文章开头的定义所示。在 grammar 定义中，语言的合法语句集合就是将 t 进行一步或多步展开（derivation）所能够得到的不包含未展开的 t 的语句的集合。在每一步展开时，我们都将当前的语句中的 t 替换成 ::= 右边的某一个语句。例如，if true then succ true else false 是一个符合语言 syntax 的语句，因为有如下的展开：

t
-> if t then t else t
-> if true then t else t
-> if true then succ t else t
-> if true then succ true else t
-> if true then succ true else false

利用数学语言，我们则可以得到三种更为精确的对 syntax 的定义：

Define Inductively

The set of terms is the smallest set T such that:

1. \left\{\text{true}, \text{false}, \text{0}\right\} \subseteq T;
2. If t_1 \in T, then \left\{\text{succ}\;t_1, \text{pred}\;t_1, \text{iszero}\;t_1\right\} \subseteq T;
3. If t_1 \in T, t_2 \in T and t_3 \in T, then \left\{\text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3\right\} \subseteq T.

这个定义很容易理解。需要注意的是定义中的 smallest 一词。Smallest 一词说明除了由上述三条规则所规定的 T 的元素之外，T 不包含其他的元素。

Define by Inference Rules

The set of terms is defined by the following rules:

1. \text{true} \in T;
2. \text{false} \in T;
3. \text{0} \in T;
4. \frac{t_1 \in T}{\text{succ}\;t_1 \in T};
5. \frac{t_1 \in T}{\text{pred}\;t_1 \in T};
6. \frac{t_1 \in T}{\text{iszero}\;t_1 \in T};
7. \frac{t_1 \in T\;\;\;t_2 \in T\;\;\; t_3 \in T}{\text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3 \in T}.

上面的定义中使用了逻辑推理中的 \frac{A}{B} 记号，其中 A 称为 premises，B 称为 conclusion。\frac{A}{B} 的含义为，如果 A 成立，那么 B 也成立。

Define Concretely

For each natural number i, define a set S_i as follows:

• S_0 = \empty;
• S_{i+1} = \left\{\text{true},\text{false},\text{0}\right\} \cup \left\{\text{succ}\;t_1,\text{pred}\;t_1,\text{iszero}\;t_1 | t_1 \in S_i\right\} \cup \left\{\text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3 | t_1,t_2,t_3 \in S_i\right\}

Finally, let S = \cup_{i}{S_i}.

Induction on Terms

我们可以定义出几个有关 term 的基本量。

首先，定义 size\left(t\right) 表示 t 构成的抽象语法树中节点的数量。即：

\begin{aligned} size\left(\text{true}\right) &= 1 \\ size\left(\text{false}\right) &= 1 \\ size\left(0\right) &= 1 \\ size\left(\text{succ}\;t_1\right) &= size\left(t_1\right) + 1 \\ size\left(\text{pred}\;t_1\right) &= size\left(t_1\right) + 1 \\ size\left(\text{iszero}\;t_1\right) &= size\left(t_1\right) + 1 \\ size\left(\text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3\right) &= size\left(t_1\right) + size\left(t_2\right) + size\left(t_3\right) + 1 \end{aligned}

其次，定义 depth\left(t\right) 表示 t 构成的抽象语法树的高度。即：

\begin{aligned} depth\left(\text{true}\right) &= 1 \\ depth\left(\text{false}\right) &= 1 \\ depth\left(0\right) &= 1 \\ depth\left(\text{succ}\;t_1\right) &= depth\left(t_1\right) + 1 \\ depth\left(\text{pred}\;t_1\right) &= depth\left(t_1\right) + 1 \\ depth\left(\text{iszero}\;t_1\right) &= depth\left(t_1\right) + 1 \\ depth\left(\text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3\right) &= \text{max}\left(depth\left(t_1\right),depth\left(t_2\right),depth\left(t_3\right)\right) + 1  \end{aligned}

为了证明关于 term 的某个性质 P，可以有三种通用的基于数学归纳法的方法：

Induction on Depth

If, for each term s, given P\left(r\right) for all r such that depth\left(r\right) < depth\left(s\right) we can show P\left(s\right), then P\left(s\right) holds for all s.

Induction on Size

If, for each term s, given P\left(r\right) for all r such that size\left(r\right) < size\left(s\right) we can show P\left(s\right), then P\left(s\right) holds for all s.

Structural Inductions

If, for each term s, given P\left(r\right) for all immediate sub-terms r of s we can show P\left(s\right), then P\left(s\right) holds for all s.

Semantics

存在三种形式化地规定语言的 semantics 的方法，分别是 operational semantics、denotational semantics 以及 axiomatic semantics。

Operational Semantics

操作语义（operational semantics）通过为语言定义一个 abstract machine 来定义语言中各个语句的语义。这里 abstract 代表这个抽象机以被描述的语言的语句作为机器代码。

在操作语义的描述中，abstract machine 被定义为一个状态机。它在某一时刻的状态由语言中的一条语句表示，这条语句就是 abstract machine 即将执行的语句。Abstract machine 的各种状态之间规定了状态转移函数，状态转移函数描述了当 abstract machine 处于某个状态时，经过单步执行后，abstract machine 的状态是什么。即，abstract machine 的状态转移函数规定了语言中的各条语句经过单步执行后会被求值为哪一条语句。

在后面的 evaluation 一节中，将详细介绍本章给出的 mini language 的 operational semantics。

Denotational Semantics

符号语义（denotational semantics）相对于操作语义是一种更加抽象的定义语言 semantics 的方法。首先，符号语义在数学上定义了一个 semantic domain；然后，符号语义定义了一个解释函数（interpretation function），解释函数负责将语言的各个语句映射到了 semantic domain 中的元素上，各个语句被映射到的 semantic domain 中的元素就是语句的 semantics。

为编程语言找寻合适的 semantic domain 以满足编程语言提供的抽象是在符号语义的定义中最具挑战性的问题。对这一问题的研究工作甚至促进了一个名为 domain theory 的数学分支的发展。

Axiomatic Semantics

公理语义（axiomatic semantics）在 TaPL 中没有作详细介绍。

Evaluation

本节详细讨论了本章开头给出的 mini language 的 operational semantics。

Operational Semantics of Boolean Expressions

我们首先只考虑 mini language 中涉及 boolean 表达式的部分的 operational semantics。这一部分的 operational semantics 可以定义如下：

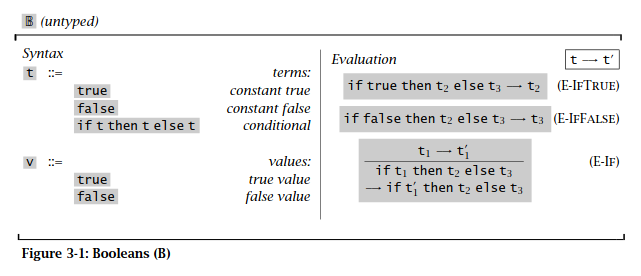
上图对 operational semantics 的定义分为了两列。其中左列给出了 boolean 表达式的语法，这里 t 表示一个 boolean 表达式，v 则表示表达式的值（value）。值是 abstract machine 对语句求值的最终结果，当 abstract machine 的状态是一个值时，abstract machine 停机。

上图中右列则定义了 operational semantics 中的求值关系（evaluation relation）。求值关系就是 abstract machine 的状态转移函数。在上图中，求值关系由三条推导规则（inference rule）组成，分别是 E-IfTrue、E-IfFalse 和 E-If。这三条推导规则中频繁使用了 A \rightarrow B 这一记号，这一记号表示语句 A 可以被 abstract machine 单步求值变为语句 B。例如，E-IfTrue 表示 abstract machine 可以在执行一步求值后将语句 \text{if}\;\text{true}\;\text{then}\;t_2\;\text{else}\;t_3 变为 t_2。另外，在 E-If 中还使用了 \frac{A}{B} 这一记号，在这一记号中 A 是一个集合，称为 premises；B 称为 conclusion。这一记号表示当 A 中的所有元素均成立时，B 也成立。例如，E-If 规则表示，如果 t_1 可以在单步求值后变为 t_1^\prime，那么语句 \text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3 也可以在单步求值后变为 \text{if}\;t_1^\prime\;\text{then}\;t_2\;\text{else}\;t_3。其实 E-IfTrue 和 E-IfFalse 也可以写作 \frac{A}{B} 记号，只不过此时 A 是空集。

在上图给出的三条推导规则中，前两条推导规则称为公理（axiom），因为它们的 premises 是空集；而最后一条推导规则称为规则（rule）。在逻辑推理中，当我们得知一个逻辑系统中所有的公理以及所有的推导规则后，我们便可以推出这个逻辑系统中所有的真命题；类似地，当我们知道 E-IfTrue、E-IfFalse 这两条公理以及 E-If 这条推导规则后，我们便可以推出 operational semantics 中定义的对任意一条语句的求值规则。

基于以上的讨论，我们来看看基于上述的 operational semantics 规定，abstract machine 应该如何求值如下的语句：

if true then (if false then false else false) else true

需要注意到的一点是，受“括号会影响运算优先级”这一根深蒂固的观念的影响，我们很容易想当然地认为我们应该首先求值括号内的内容，从而将上述语句化简为 if true then false else true。然而，求值关系中并没有规定有如此的规则，abstract machine 只能使用上图中提供的三条推导规则来一步步地化简和求值整条语句。括号的存在只是为了避免 syntax parsing 过程中出现二义性，而与求值的顺序、步骤没有直接关联。因此，abstract machine 在执行的第一步只能套用 E-IfTrue 规则，将语句变为如下形式：

if false then false else false

然后，我们可以套用 E-IfFalse 规则，将语句变为如下形式：

false

至此，没有任何的推导规则能够化简这个语句，且 false 已经是一个值（value）。因此 abstract machine 停机，求值结束。

我们还可以注意到一个有趣的地方。E-IfTrue 和 E-IfFalse 这两条推导规则可以视作“真正”的求值，因为它们都消除了语句顶层的 if then else 结构；而 E-If 这条推导规则没有改变语句的结构，它只是将语句朝着能够应用 E-IfTrue 和 E-IfFalse 这两条推导规则进行化简的方向进行变换。因此，我们将 E-IfTrue 和 E-IfFalse 这样的推导规则称为计算规则（computation rule），将 E-If 这样的规则称为一致性规则（congruence rule）。

Formal Definitions of One-Step Evaluation Relation

Instance of an inference rule

Definition: an instance of an inference rule is obtained by consistently replacing each metavariable by the same term in the rule’s conclusion and all its premises (if any).

推导规则的实例（instance）的定义很容易理解。我们只需要将推导规则中的所有元变量（metavariable），例如 t、t_1、t_2 等，不断替换为具体的语句便可以得到推导规则的所有实例。例如，对于推导规则 \text{if}\;\text{true}\;\text{then}\;t_2\;\text{else}\;t_3 \rightarrow t_2，我们可以得到以下的一些实例：

t2 :: true, t3:: true
if true then true else true -> true

t2 :: if false then false else true, t3 :: false
if false then (if false then false else true) else false -> false

t2 :: true, t3 :: if true then true else true
if false then true else (if true then true else true) -> if true then true else true

Relation satisfies a rule

Definition: a rule is satisfied by a relation if, for each instance of the rule, either the conclusion is in the relation or one of its premises is not.

这一条定义在初次理解时有一定的困难。为了弄清这条定义的含义，我们需要再次回顾一下定义中的 relation 和 rule 这两个词的含义。

首先，relation 可以等同于 abstract machine 的状态转移函数。如果我们将程序的所有可能的语句定义为一个集合 S，那么 relation 就是一个 S \rightarrow S 的二元关系。这个二元关系将 S 中的某些语句（那些不是值的语句）映射到 S 中的另一些语句上，反映了 abstract machine 在单步执行某条语句后得到的新语句。Relation 也可以视为一个集合，它的元素具有 A \rightarrow B 的形式，表示 relation 将语句 A 映射到了语句 B 上。

其次，一条 rule 就是图 3-1 中在右列定义的一条推导规则。一条 rule 始终可以写作 \frac{A}{B} 的形式，其中 A 称为 premises，B 称为 conclusion，其含义在上一节中已经详细介绍了。作为公理存在的 rule 可能没有 premises，即 A 是空集，例如 E-IfTrue 和 E-IfFalse。

这一条定义则是说当 relation 的某个子集符合某一条 rule 所定义的推导规则时，我们可以称这个 relation 满足（satisfy）了某一条 rule。更加严格地，这一条定义还说明了我们应该如何考察 relation 是否满足某一条 rule。考察这一点需要 rule 的所有实例均满足两个条件中的一个：

1. 如果 rule 实例的 conclusion 在 relation 中；
2. 如果 rule 实例的某一条 premises 不在 relation 中。

我们不妨用一个例子来理解这两个条件。考虑 E-If 这一条 rule：

\frac{t_1 \rightarrow t_1^\prime}{\text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3 \rightarrow \text{if}\;t_1^\prime\;\text{then}\;t_2\;\text{else}\;t_3}

我们考虑它的两个 instance：

t1 :: if true then true else false, t1' :: true, t2 :: true, t3 :: false
if true then true else false -> true
------------------------------------
if (if true then true else false) then true else false -> if true then true else false

t1 :: true, t1' :: false, t2 :: true, t3 :: false
true -> false
-------------
if true then true else false -> if false then true else false

对于第一个 instance，它的 conclusion if (if true then true else false) then true else false -> if true then true else false 显然在 relation 中，那么此时 relation 是满足这个 instance 的；对于第二个 instance，它的 conclusion if true then true else false -> if false then true else false 并不在 relation 中，那么此时一定有至少一个 premise 不在 relation 中，即 true -> false 这一个 premise。此时 relation 仍然满足这个 instance，因为这个 instance 根本无法应用到求值过程中。

One-Step Evaluation Relation & Derivable Statements

Definition: the one-step evaluation relation \rightarrow is the smallest binary relation on terms satisfying the three rules in Figure 3-1. When the pair \left(t, t^\prime\right) is in the evaluation relation, we say that “the evaluation statement (or judgment) t \rightarrow t^\prime is derivable.”

这个定义给出了基于图 3-1 中给出的三条推导规则的 one-step evaluation relation 是什么。在理解了什么叫做 relation 满足 rule 后，这个定义很容易理解。需要注意的是定义中使用的 smallest 一词，smallest 这一属性说明定义得到的 relation 是一个 one-step evaluation relation，即这个 relation 只将程序语句映射到经过 abstract machine 单步执行后得到的语句，而不包含那些经过了多步执行的 evaluation relation。

Derivable statements 的定义非常简单。如果语句 t 可以基于 one-step evaluation relation 通过单步求值变为 t^\prime，那么 t \rightarrow t^\prime 这一个 statement 便是 derivable 的。

Derivation Tree

我们可以借助 derivation tree 来判断一个 statement 是否是 derivable 的。

考虑下面的这一条十分复杂的 statement：

s :: if true then false else false
t :: if s then true else true
u :: if false then true else true
if t then false else false -> if u then false else false

s、t 和 u 是为了方便书写而引入的符号。

为了判断 if t then false else false -> if u then false else false 这一条 statement 是否是 derivable 的，我们可以画出如下所示的 derivation tree：

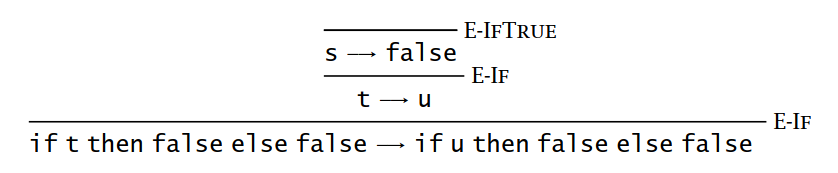
Derivation tree 可以从上往下阅读。首先，利用 E-IfTrue 公理，我们知道 \text{s} \rightarrow \text{false} 是 derivable 的；然后，利用 E-If 规则，将 \text{s} \rightarrow \text{false} 作为 premise，我们可以得出 \text{t} \rightarrow \text{u} 是 derivable 的；最后，再次利用 E-If 规则，将 \text{t} \rightarrow \text{u} 作为 premise，我们可以得出 if t then false else false -> if u then false else false 这一条 statement 是 derivable 的。

Derivation tree 从叶节点到根节点模拟了逻辑推理的全过程，即从一个在叶节点上的公理开始，不断应用推导规则，最终得到需要考察的 statement。因此，derivation tree 的叶节点上均是公理，derivation tree 的内部节点上则都是规则。另外，在下一节我们将知晓 one-step evaluation 是没有歧义的，即同一条语句经过单步执行最多只能得到一条语句，因此 derivation tree 其实是一条单链，并没有树分支。

Determinacy of One-Step Evaluation

Theorem: If \text{t} \rightarrow \text{t}^\prime and \text{t} \rightarrow \text{t}^{\prime\prime}, then \text{t}^\prime = \text{t}^{\prime\prime}.

这一条定理说明了本章定义的 one-step evaluation 是无歧义的。即 evaluation relation 不会将同一条语句映射到两条不同的语句。

这个定理的证明是比较简单的，只需要将 \text{t} 分情况讨论即可。

Normal Forms

Definition: A term \text{t} is in normal form if no evaluation rules apply to it — i.e. if there is no \text{t}^\prime such that \text{t} \rightarrow \text{t}^\prime.

Normal form 的定义很直接，即那些无法再被求值的语句。

下面两条重要的定理则说明了 normal form 和 value 的“全等”关系：

Theorem: Every value is in normal form.

Theorem: If \text{t} is in normal form, then \text{t} is a value.

首先，每一个值都是 normal form 这个定理是非常容易证明的，因此不再讨论。其次，对于所有的 normal form 都是值这个定理，我们可以利用前面介绍的 induction on depth 进行证明。

• 基本情况：当 depth\left(\text{t}\right) = 1 时，此时 \text{t} = \text{true} 或 \text{t} = \text{false}，此时结论显然成立；
• 归纳情况：现在不妨假设 depth\left(\text{t}\right) > 1，且对于所有的深度小于 depth\left(t\right) 的语句 \text{r}，都有原结论成立。此时一定有 \text{t} = \text{if}\;t_1\;\text{then}\;t_2\;\text{else}\;t_3，因此 \text{t} 一定不是值，我们只需要证明 \text{t} 不是 normal form 即可。我们考察 t_1 的情况，t_1 一定有 depth\left(t_1\right) < depth\left(t\right)。若 t_1 = \text{true} 或 t_1 = \text{false}，那么此时 \text{t} 显然不是 normal form，因为此时可以直接应用 E-IfTrue 或 E-IfFalse 规则对 \text{t} 进行求值；若 1 < depth\left(t_1\right) < depth\left(\text{t}\right)，那么由前提条件，此时 t_1 不是 normal form，因此一定存在一个 t_1^\prime 使得 t_1 \rightarrow t_1^\prime。此时 E-If 规则可以用于求值 \text{t}，因此此时 \text{t} 也不是 normal form。综上，\text{t} 不是 normal form，原命题得证。

Multi-Step Evaluation Relation

Definition: The multi-step evaluation relation \rightarrow^ is the reflexive, transitive closure of one-step evaluation. That is, it is the smallest relation such that: (1) if \text{t} \rightarrow \text{t}^\prime, then \text{t} \rightarrow^ \text{t}^\prime; (2) \text{t} \rightarrow^* \text{t} for all \text{t}; (3) if \text{t} \rightarrow^* \text{t}^\prime and \text{t}^\prime \rightarrow^* \text{t}^{\prime\prime}, then \text{t} \rightarrow^* \text{t}^{\prime\prime}.

Multi-step evaluation relation 的定义很容易理解，在此不讨论。

下面的定理则说明了 abstract machine 一定会停机，即所有的语句都最终会被 abstract machine 求值为一个值：

Theorem: for every form \text{t} there is some normal form \text{t}^\prime such that \text{t} \rightarrow \text{t}^\prime.

这个定理的证明也比较简单。注意到 size\left(\text{true}\right) = size\left(\text{false}\right) = 1 ，且在单步执行的每一步，语句的 size 是严格递减的。因此所有语句最终都会被求值为 \text{true} 或者 \text{false}。

下面的定理则说明了 abstract machine 对任意语句求值的最终结果一定是唯一的：

Theorem: If \text{t} \rightarrow^* \text{u} and \text{t} \rightarrow^* \text{u}^\prime, where \text{u} and \text{u}^\prime are both normal forms, then \text{u} = \text{u}^\prime.

这一条定理比较容易证明。基本想法是由于单步求值的每一步都是确定的，因此在对语句进行多步求值后得到的最终结果一定也是唯一的。

Operational Semantics of Arithmetic Expressions

我们已经讨论完毕 boolean 表达式的 operational semantics。现在我们可以开始考虑 mini language 中有关数值运算部分的 operational semantics。这一部分的 operational semantics 如下图所示：

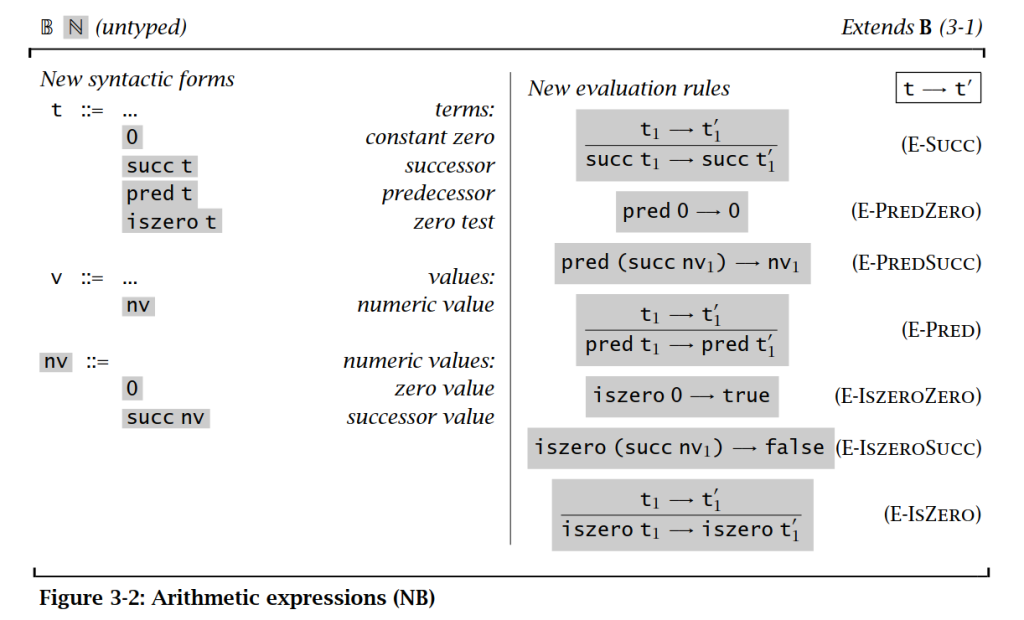
与 boolean 表达式的 operational semantics 相比，上图扩展的 operational semantics 并没有增加全新的内容，只是扩充了原本的 syntax 和推导规则。但是，上图中的 operational semantics 使用了一些技巧来避免求值过程出现歧义。例如，上图的 operational semantics 规定了一个全新的 value 类别 nv，用于表示数值的值。在推导规则 E-PredSucc 中，没有使用 pred (succ t) -> t，而是使用了 pred (succ nv) -> nv。这是为了避免在求值类似于如下的语句时出现歧义：pred (succ (pred 0))。当 E-PredSucc 是 pred (succ nv) -> nv 时，只有如下列 derivation tree 所示的唯一一种求值路线：

Stuckness

在本章最后提出了 stuck 的概念：

Definition: a closed term is stuck if it is in normal form but not a value.

Stuck 的语句是 abstract machine 中的“无意义”的状态，因为 abstract machine 无法进一步求值这些语句。这些 stuck 的语句可以被语言用于抽象错误 / 异常等特性。